
Five years from now, you'll probably wish you'd started investing with Stock Advisor
- New stock picks each month
- Detailed analysis of companies
- Model portfolios and advanced tools
- Live streaming during market hours
Featured Investing News


The House Just Passed the TikTok Ban. Here's What That Means for Meta Stock.

Why I Sold These 3 Tech Stocks in 2024

Should You Buy a Spot Bitcoin ETF After the Halving?

4 Reasons to Buy Carnival Stock Like There's No Tomorrow
Trending News
- I Was Incredibly Wrong About the Tesla Cybertruck
- This Is Hands Down My Pick for the Best "Magnificent Seven" Stock Right Now. (Hint: It's Not Nvidia.)
- The Social Security COLA Countdown Is On: Here's How Much Your Increase Will Likely Be as Things Stand Right Now
- It's Time to Ditch These 2 "Magnificent Seven" Stocks and Replace Them With 2 Bona Fide Outperformers
- The Bond Market Is Sounding Its Most Severe Alarm in Decades, and It Could Mean Trouble for the Stock Market
- Forget Nvidia: Billionaires Are Selling It and Buying These 2 High-Octane Artificial Intelligence (AI) Growth Stocks Instead
- With Shares Down Nearly 70%, I'm Piling Into this Ultra-High-Yield Dividend Stock
- Down 80%, Is Carnival Stock a Once-in-a-Generation Investment Opportunity?
- Time to Pounce: 2 Phenomenal Ultra-High-Yield REITs That Haven't Been This Cheap in Years
- 1 No-Brainer Vanguard Fund to Buy Right Now
- 1 No-Brainer ETF to Buy With $100 Right Now
- TSMC Just Gave Investors Another Reason to Be Bullish on Nvidia
- The UItimate Cryptocurrency to Buy With $1,000 Today
- 2 Artificial Intelligence (AI) Stocks That Could Fall 19% and 65%, According to a Pair of Wall Street Analysts
- Should You Buy Microsoft Stock Before Thursday?
Popular Topics
About The Motley Fool
Our Purpose: To make the world smarter, happier, and richer.
Founded in 1993 by brothers Tom and David Gardner, The Motley Fool helps millions of people attain financial freedom through our website, podcasts, books, newspaper column, radio show, and premium investing services. We believe that investing is empowering, enriching, and fun. We look forward to joining you on your journey to financial independence. Learn More
The Motley Fool Investing Philosophy
Learn How We Invest-
#1 Buy 25+ Companies Over Time
-
#2 Hold Stocks for 5+ Years
-
#3 Add New Savings Regularly
-
#4 Hold Through Market Volatility
-
#5 Let Your Winners Run
-
#6 Target Long-Term Returns
Investing Solutions Designed To Make Money Over The Long Term
Become a member today

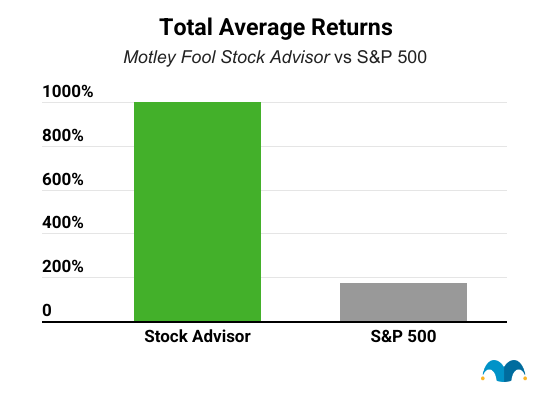
Stock Advisor
Our base-level-membership giving you the foundation of a Foolish portfolio
Help members earn a positive return and build the foundations of a portfolio backed by Motley Fool principles.
Individuals who are seeking easy-to-use guidance on investing in more familiar-named companies.
$5,000 +
- Monthly stock recommendations (usually large and mid-cap stocks)
- Portfolio allocation guidance via The Motley Fool's Allocator tool
- On-going coverage of prior recommendations
- Access to Motley Fool Live video stream

Epic Bundle
A bundled membership that combines our four foundational stock-investing services into one
Help members outperform the benchmark by gaining exposure to a wider variety of stocks and investments.
Individuals who are regularly adding new money to their brokerage accounts, interested in business, and want to spend more time learning the art of investing.
$25,000 +
- Includes access to Stock Advisor + Rule Breakers + Everlasting Stocks + Real Estate Winners
- Weekly stock recommendations (ranging from small to large-cap stocks)
- Portfolio allocation guidance via The Motley Fool's Allocator tool
- On-going coverage of prior recommendations from all included services
- Access to Motley Fool Live video stream