
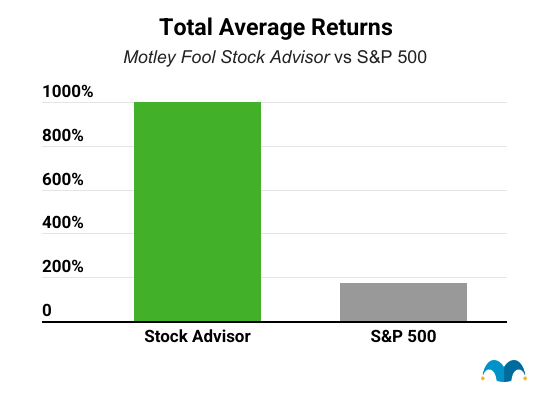
Five years from now, you'll probably wish you'd started investing with Stock Advisor
- New stock picks each month
- Detailed analysis of companies
- Model portfolios and advanced tools
- Live streaming during market hours
Featured Investing News


3 Top Tech Stocks to Buy in April

Microsoft Invests $1.5 Billion in an AI Company: Here's What Investors Should Know

Got $500? 3 Healthcare Stocks to Buy and Hold Forever

3 No-Brainer Bank Stocks to Buy With $1,000 Right Now
Trending News
- Forget Nvidia: 2 Super Semiconductor Stocks to Buy Hand Over Fist, According to Wall Street
- 2 Popular Artificial Intelligence (AI) Stocks to Sell Before They Drop 29% and 77%, According to Certain Wall Street Analysts
- 2 No-Brainer Vanguard ETFs to Buy With $750 During the Stock Market Sell-Off
- Why Super Micro Computer Stock Just Crashed 17%
- I Used to Think 65 Was the Best Age to Retire. Here's Why I've Changed My Mind.
- 3 Vanguard Funds That Can Serve as a Complete Portfolio
- Time to Pounce: 2 Superb Utility Stocks That Haven't Been This Cheap in at Least 10 Years
- If I Could Buy Only 3 Stocks in 2024, I'd Pick These
- Opinion: These Will Be the 4 Largest Companies by 2035
- Meet the Stock-Split Stock Making Wall Street History, Plus the Nasdaq Stock That Could Split Next
- Prediction: This Artificial Intelligence (AI) Stock Could Be Worth More Than Microsoft 5 Years From Now
- Want to Outperform 88% of Professional Fund Managers? Buy This 1 Investment and Hold It Forever.
- 1 Warren Buffett ETF to Buy and Hold Forever
- Billionaire Bill Gates Is Betting $7.1 Billion on This 1 Famous Stock
- Warren Buffett Has Over $10 Billion Invested in 7 Stocks. Here's the Best Stock to Buy Right Now, According to Wall Street.
Popular Topics
About The Motley Fool
Our Purpose: To make the world smarter, happier, and richer.
Founded in 1993 by brothers Tom and David Gardner, The Motley Fool helps millions of people attain financial freedom through our website, podcasts, books, newspaper column, radio show, and premium investing services. We believe that investing is empowering, enriching, and fun. We look forward to joining you on your journey to financial independence. Learn More
The Motley Fool Investing Philosophy
Learn How We Invest-
#1 Buy 25+ Companies Over Time
-
#2 Hold Stocks for 5+ Years
-
#3 Add New Savings Regularly
-
#4 Hold Through Market Volatility
-
#5 Let Your Winners Run
-
#6 Target Long-Term Returns
Investing Solutions Designed To Make Money Over The Long Term
Become a member today

Stock Advisor
Our base-level-membership giving you the foundation of a Foolish portfolio
Help members earn a positive return and build the foundations of a portfolio backed by Motley Fool principles.
Individuals who are seeking easy-to-use guidance on investing in more familiar-named companies.
$5,000 +
- Monthly stock recommendations (usually large and mid-cap stocks)
- Portfolio allocation guidance via The Motley Fool's Allocator tool
- On-going coverage of prior recommendations
- Access to Motley Fool Live video stream

Epic Bundle
A bundled membership that combines our four foundational stock-investing services into one
Help members outperform the benchmark by gaining exposure to a wider variety of stocks and investments.
Individuals who are regularly adding new money to their brokerage accounts, interested in business, and want to spend more time learning the art of investing.
$25,000 +
- Includes access to Stock Advisor + Rule Breakers + Everlasting Stocks + Real Estate Winners
- Weekly stock recommendations (ranging from small to large-cap stocks)
- Portfolio allocation guidance via The Motley Fool's Allocator tool
- On-going coverage of prior recommendations from all included services
- Access to Motley Fool Live video stream